一切福田，不離方寸，從心而覓，感無不通。

DES/3DES/AES区别

DES

1977年1月，美国政府颁布：采纳IBM公司设计的方案作为非机密数据的正式数据加密标准（DES Data Encryption Standard) 。

目前在国内，随着三金工程尤其是金卡工程的启动，DES算法在POS、ATM、磁卡及智能卡（IC卡）、加油站、高速公路收费站等领域被广泛应用，以此来实现关键数据的保密，如信用卡持卡人的PIN的加密传输，IC卡与POS间的双向认证、金融交易数据包的MAC校验等，均用到DES算法。

DES算法的入口参数有三个：Key、Data、Mode。

其中Key为8个字节共64位，是DES算法的工作密钥；

Data也为8个字节64位，是要被加密或被解密的数据；

Mode为DES的工作方式，有两种：加密或解密。

DES算法是这样工作的：

如Mode为加密，则用Key 去把数据Data进行加密， 生成Data的密码形式（64位）作为DES的输出结果；

如Mode为解密，则用Key去把密码形式的数据Data解密，还原为Data的明码形式（64位）作为DES的输出结果。

在通信网络的两端，双方约定一致的Key，在通信的源点用Key对核心数据进行DES加密，然后以密码形式在公共通信网（如电话网）中传输到通信网络的终点，数据到达目的地后，用同样的Key对密码数据进行解密，便再现了明码形式的核心数据。这样，便保证了核心数据（如PIN、MAC等）在公共通信网中传输的安全性和可靠性。

通过定期在通信网络的源端和目的端同时改用新的Key，便能更进一步提高数据的保密性，这正是现在金融交易网络的流行做法。

 

 

3DES

3DES是DES加密算法的一种模式，它使用3条64位的密钥对数据进行三次加密。数据加密标准（DES）是美国的一种由来已久的加密标准，它使用对称密钥加密法。

3DES（即Triple DES）是DES向AES过渡的加密算法（1999年，NIST将3-DES指定为过渡的加密标准），是DES的一个更安全的变形。它以DES为基本模块，通过组合分组方法设计出分组加密算法。

设Ek()和Dk()代表DES算法的加密和解密过程，K代表DES算法使用的密钥，P代表明文，C代表密表，这样，

3DES加密过程为：C=Ek3(Dk2(Ek1(P)))

3DES解密过程为：P=Dk1((EK2(Dk3(C)))

K1、K2、K3决定了算法的安全性，若三个密钥互不相同，本质上就相当于用一个长为168位的密钥进行加密。多年来，它在对付强力攻击时是比较安全的。若数据对安全性要求不那么高，K1可以等于K3。在这种情况下，密钥的有效长度为112位。

AES

AES(Advanced Encryption Standard)：高级加密标准，是下一代的加密算法标准，速度快，安全级别高。

用AES加密2000年10月，NIST（美国国家标准和技术协会）宣布通过从15种候选算法中选出的一项新的密匙加密标准。Rijndael被选中成为将来的 AES。Rijndael是在1999年下半年，由研究员Joan Daemen 和 Vincent Rijmen 创建的。AES正日益成为加密各种形式的电子数据的实际标准。

美国标准与技术研究院（NIST）于2002年5月26日制定了新的高级加密标准（AES）规范。

AES算法基于排列和置换运算。排列是对数据重新进行安排，置换是将一个数据单元替换为另一个。

AES使用几种不同的方法来执行排列和置换运算。AES是一个迭代的、对称密钥分组的密码，它可以使用128、192和256位密钥，并且用128位（16字节）分组加密和解密数据。

与公共密钥加密使用密钥对不同，对称密钥密码使用相同的密钥加密和解密数据。通过分组密码返回的加密数据的位数与输入数据相同。迭代加密使用一个循环结构，在该循环中重复置换和替换输入数据。

算法   Key                  位数                 可逆?                其它
MD5    没有Key,             有区别16位和32位,    不可逆               (无)
SHA    （？）              （？）                不可逆               (无)
RSA    有（公Key,私KEY）   （？）                可逆                 公、私Key采用不同的加密算法
DES3   有                  （？）                可逆                 (无)
AES    有                  （？）                可逆                 (无)
BASE64 没有KEY             （？）                可逆                 (无)

哈希函数,比如MD5,SHA，这些都不是加密算法。要注意他们的区别和用途，很多网友都把md5说成是加密算法，这是严重不正确的啊。

哈希函数：MD5，SHA 是没有密钥的，相当与指纹的概念，因此也是不可逆的；
md5是128位的，SHA有不同的算法，有128，256等位。。。如SHA-256,SHA-384
然后 就是 Base64,这更加不属于加密算法的范围了，它只是将byte[]数组进行了转换，为什么要转换呢？就是因为很多加密后的密文后者一些特殊的byte[]数组需要显示出来，或者需要进行传递（电子邮件），但是直接转换就会导致很多不可显示的字符，会丢失一些信息，因此就转换位Base64编码，这些都是可显示的字符。所以转换后，长度会增加。它是可逆的。

再就是 3DES,DES 这才是加密算法，因此也是可逆的，加解密需要密钥,也就是你说的key

最后是 RSA ,这是公钥密码，也就是加密和解密密钥不同，也是可逆的。

DES算法：

DES算法把64位的明文输入块变为64位的密文输出块，它所使用的密钥也是64位，整个算法的主流程图如下：
其功能是把输入的64位数据块按位重新组合，并把输出分为L0、R0两部分，每部分各长32位，其置换规则见下表：
58,50,12,34,26,18,10,2,60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8,
57,49,41,33,25,17, 9,1,59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7,
即将输入的第58位换到第一位，第50位换到第2位，…，依此类推，最后一位是原来的第7位。L0、R0则是换位输出后的两部分，L0是输出的 左 32位，R0 是右32位，例：设置换前的输入值为D1D2D3……D64，则经过初始置换后的结果 为：L0=D58D50…D8；R0= D57D49…D7。
经过16次迭代运算后。得到L16、R16，将此作为输入，进行逆置换，即得到密文输出。逆置换正好是初始置的逆运算，例如，第1位经过初始置换后，处于第40位，而通过逆置换，又将第40位换回到第1位，其逆置换规则如下表所示：
40,8,48,16,56,24,64,32,39,7,47,15,55,23,63,31,
38,6,46,14,54,22,62,30,37,5,45,13,53,21,61,29,
36,4,44,12,52,20,60,28,35,3,43,11,51,19,59,27,
34,2,42,10,50,18,58 26,33,1,41, 9,49,17,57,25,
放大换位表
32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9, 8, 9, 10,11,
12,13,12,13,14,15,16,17,16,17,18,19,20,21,20,21,
22,23,24,25,24,25,26,27,28,29,28,29,30,31,32, 1,
单纯换位表
16,7,20,21,29,12,28,17, 1,15,23,26, 5,18,31,10,
2,8,24,14,32,27, 3, 9,19,13,30, 6,22,11, 4,25,
在f(Ri,Ki)算法描述图中，S1,S2…S8为选择函数，其功能是把6bit数据变为4bit数据。下面给出选择函数Si(i=1,2……8)的功能表：
选择函数Si
S1:
14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7,
0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8,
4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0,
15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13,
S2:
15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10,
3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5,
0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15,
13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9,
S3:
10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8,
13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1,
13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7,
1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12,
S4:
7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15,
13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9,
10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4,
3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14,
S5:
2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9,
14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6,
4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14,
11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3,
S6:
12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11,
10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8,
9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6,
4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13,
S7:
4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1,
13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6,
1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2,
6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12,
S8:
13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7,
1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2,
7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8,
2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11,
在此以S1为例说明其功能，我们可以看到：在S1中，共有4行数据，命名为0，1、2、3行；每行有16列，命名为0、1、2、3，……，14、15列。
现设输入为： D＝D1D2D3D4D5D6
令：列＝D2D3D4D5
行＝D1D6
然后在S1表中查得对应的数，以4位二进制表示，此即为选择函数S1的输出。下面给出子密钥Ki(48bit)的生成算法
从子密钥Ki的生成算法描述图中我们可以看到：初始Key值为64位，但DES算法规定，其中第8、16、……64位是奇偶校验位，不参 与 DES运算。故Key 实际可用位数便只有56位。即：经过缩小选择换位表1的变换后，Key 的位数由64 位变成了56位，此56位分为C0、 D0两部分，各28位，然后分别进行第1次循环左移，得到C1、D1，将C1（28位）、D1（28位）合并得到56 位，再经过缩小选择换位2，从而便 得到了密钥K0（48位）。依此类推，便可得到K1、K2、……、K15，不过需要注意的是，16次循环左移对应的左移位数要依据下述规则进行：
循环左移位数
1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1
以上介绍了DES算法的加密过程。DES算法的解密过程是一样的，区别仅仅在于第一次迭代时用子密钥K15，第二次K14、……，最后一次用K0，算法本身并没有任何变化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
//DES算法加密
#include<iostream>
#include<math.h>
using namespace std;
char * str2bin(char *str){//将16位16进制码转换为64位二进制码(不足8位高位补0)
    int i;
    char *st2;
    st2=(char*)malloc(sizeof(char)*65);
    st2[0]='\0';
    for(i=0;i<16;i++){
        switch(str[i]){
        case '0':strcat(st2,"0000");break;
        case '1':strcat(st2,"0001");break;
        case '2':strcat(st2,"0010");break;
        case '3':strcat(st2,"0011");break;
        case '4':strcat(st2,"0100");break;
        case '5':strcat(st2,"0101");break;
        case '6':strcat(st2,"0110");break;
        case '7':strcat(st2,"0111");break;
        case '8':strcat(st2,"1000");break;
        case '9':strcat(st2,"1001");break;
        case 'A':strcat(st2,"1010");break;
        case 'B':strcat(st2,"1011");break;
        case 'C':strcat(st2,"1100");break;
        case 'D':strcat(st2,"1101");break;
        case 'E':strcat(st2,"1110");break;
        case 'F':strcat(st2,"1111");break;
        }
    }
    st2[64]='\0';
    return st2;
}
char * bin2str(char *st2){//将64位二进制码转换为16位16进制码
    int i,j;
    char *st;
    int a[]={8,4,2,1};
    int buf;
    st=(char*)malloc(sizeof(char)*17);
    for(i=0;i<16;i++){
        buf=0;
        for(j=0;j<4;j++){
            buf=buf+(st2[i*4+j]=='1'? a[j]:0);
        }
        switch(buf){
        case 0: st[i]='0';break;
        case 1: st[i]='1';break;
        case 2: st[i]='2';break;
        case 3: st[i]='3';break;
        case 4: st[i]='4';break;
        case 5: st[i]='5';break;
        case 6: st[i]='6';break;
        case 7: st[i]='7';break;
        case 8: st[i]='8';break;
        case 9: st[i]='9';break;
        case 10: st[i]='A';break;
        case 11: st[i]='B';break;
        case 12: st[i]='C';break;
        case 13: st[i]='D';break;
        case 14: st[i]='E';break;
        case 15: st[i]='F';break;
        }        
    }
    st[16]='\0';
    return st;
}
char * chushizhihuan(char *strb){//1.初始置换
    char *stra;
    int i;
    stra=(char*)malloc(sizeof(char)*65);
    int a[64] = {57,49,41,33,25,17,9,1,
,51,43,35,27,19,11,3,
,53,45,37,29,21,13,5,
,55,47,39,31,23,15,7,
,48,40,32,24,16,8,0,
,50,42,34,26,18,10,2,
,52,44,36,28,20,12,4,
,54,46,38,30,22,14,6};
    for(i=0;i<64;i++)
        stra[i]=strb[a[i]];
    stra[i]='\0';
    return stra;
}
char* miyuezhihuan(char *keyb){//3.密钥置换
    char *keya;
    int i;
    keya=(char*)malloc(sizeof(char)*57);
    int a[]={56,48,40,32,24,16,8,
,57,49,41,33,25,17,
,1,58,50,42,34,26,
,10,2,59,51,43,35,
,54,46,38,30,22,14,
,61,53,45,37,29,21,
,5,60,52,44,36,28,
,12,4,27,19,11,3};
    for(i=0;i<56;i++){
        keya[i]=keyb[a[i]];
    }
    keya[i]='\0';
    return keya;
}
void miyuezuoyi(char *keyb,int n){//4.第n轮密钥左移
    char *temp;
    int a[]={1,1,2,2,2,2,2,2,
,2,2,2,2,2,2,1};
    temp=(char*)malloc(sizeof(char)*57);
    //保存将要循环移动到右边的位  
    memcpy(temp,keyb,a[n]);  
    memcpy(temp+a[n],keyb+28,a[n]);  
      
    //前28位移动  
    memcpy(keyb,keyb+a[n],28-a[n]);  
    memcpy(keyb+28-a[n],temp,a[n]);  
  
    //后28位移动  
    memcpy(keyb+28,keyb+28+a[n],28-a[n]);  
    memcpy(keyb+56-a[n],temp+a[n],a[n]);
}
char * miyueyasuozhihuan(char *key){//5.密钥压缩置换(产生子密钥)
    int i;
    char *keybuf;
    keybuf=(char*)malloc(sizeof(char)*49);
    int a[]={13,16,10,23,0,4,
,27,14,5,20,9,
,18,11,3,25,7,
,6,26,19,12,1,
,51,30,36,46,54,
,39,50,44,32,47,
,48,38,55,33,52,
,41,49,35,28,31};
    for(i=0;i<48;i++){
        keybuf[i]=key[a[i]];
    }
    keybuf[i]='\0';
    return keybuf;
}
char * kuozhanzhihuan(char *st){//6.扩展置换
    int i;
    char *stbuf;
    stbuf=(char*)malloc(sizeof(char)*49);
    int a[48] = {31, 0, 1, 2, 3, 4,
,  4, 5, 6, 7, 8,
,  8,9,10,11,12,
,12,13,14,15,16,
,16,17,18,19,20,
,20,21,22,23,24,
,24,25,26,27,28,
,28,29,30,31, 0};
    for(i=0;i<48;i++)
        stbuf[i]=st[a[i]];
    stbuf[i]='\0';
    return stbuf;
}
void yihuoyunsuan(char * str,char *key,int n){//7.异或运算
    int i;
    for(i=0;i<n;i++){
        str[i]=(str[i]==key[i])? '0':'1';
    }
}
int bin2int(char *bin){
    int i;
    int Int;
    Int=0;
    for(i=0;i<strlen(bin);i++)
        if(bin[i]=='1')
            Int=Int+pow(2,strlen(bin)-i-1);
    return Int;
}
char *int2bin(int Int){
    char *bin;
    int key;
    int i;
    key=8;
    bin=(char*)malloc(sizeof(char)*5);
    for(i=0;i<4;i++){
        bin[i]=(key&Int)? '1':'0' ;
        key>>=1;
    }
    bin[4]='\0';
    return bin;
}
char* Shedaiti(char *strb){//8.S盒代替
    int i,j;
    char *stra;
    char *hang;
    char *lie;
    stra=(char *)malloc(sizeof(char)*33);
    hang=(char *)malloc(sizeof(char)*3);
    lie=(char *)malloc(sizeof(char)*5);
    stra[0]='\0';
    int s[8][4][16]=//S1
              {{{14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7},
                {0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8},
                {4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0},
                {15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13}},
                //S2
                {{15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10},
                {3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5},
                {0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15},
                {13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9}},
                //S3
                {{10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8},
                {13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1},
                  {13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7},
                {1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12}},
                //S4
                {{7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15},
                {13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9},
                {10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4},
                {3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14}},
                //S5
                {{2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9},
                {14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6},
                {4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14},
                {11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3}},
                //S6
                {{12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11},
                {10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8},
                {9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6},
                {4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13}},
                //S7
                {{4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1},
                {13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6},
                {1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2},
                {6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12}},
                //S8
                {{13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7},
                {1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2},
                {7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8},
                {2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11}}};
    for(i=0;i<8;i++){
        hang[0]=strb[i*6];
        hang[1]=strb[i*6+5];
        hang[2]='\0';
        for(j=0;j<4;j++)
            lie[j]=strb[i*6+j+1];
        lie[j]='\0';
        strcat(stra,int2bin(s[i][bin2int(hang)][bin2int(lie)]));
    }
    return stra;
}
char *Phezhihuan(char *strb){//9.P盒置换
    char *stra;
    stra=(char*)malloc(sizeof(char)*33);
    int i;
    int P[]= {15,6,19,20,28,11,27,16,
,14,22,25,4,17,30,9,
,7,23,13,31,26,2,8,
,12,29,5,21,10,3,24};
    for(i=0;i<32;i++)
        stra[i]=strb[P[i]];
    stra[i]='\0';
    return stra;
}
char *hebing(char *strl,char *strr){//13.合并
    char *str;
    str=(char*)malloc(sizeof(char)*65);
    strcpy(str,strl);
    strcat(str,strr);
    return str;
}
char* nichushizhihuan(char *strb){//13.逆初始置换
    char *stra;
    int i;
    stra=(char*)malloc(sizeof(char)*65);
    int a[64]= {39,7,47,15,55,23,63,31,
,6,46,14,54,22,62,30,
,5,45,13,53,21,61,29,
,4,44,12,52,20,60,28,
,3,43,11,51,19,59,27,
,2,42,10,50,18,58,26,
,1,41,9,49,17,57,25,
,0,40,8,48,16,56,24};
    for(i=0;i<64;i++){
        stra[i]=strb[a[i]];
    }
    stra[i]='\0';
    return stra;
}
int swap(char *left, char *right){  
    char *temp;
    temp=(char *)malloc(sizeof(char)*33);
    memcpy(temp,left,32);    
    memcpy(left,right,32);    
    memcpy(right,temp,32);  
    return 0;  
}
int main(){
    int j;
    char *str_Ox;
    char *str_64;
    char *str_R_48;
    char *key_Ox;
    char *key_56;
    char *key_48;
    str_Ox = (char*)malloc(sizeof(char)*17);
    str_64 = (char*)malloc(sizeof(char)*65);
    str_R_48 = (char*)malloc(sizeof(char)*49);
    key_Ox  = (char*)malloc(sizeof(char)*17);
    key_56  = (char*)malloc(sizeof(char)*57);
    key_48  = (char*)malloc(sizeof(char)*49);while(scanf("%s %s",key_Ox,str_Ox)!=EOF){//获取16位16进制密钥和16位16进制原文
        key_56 = miyuezhihuan(str2bin(key_Ox));//将字符密钥转换为01密钥并执行密钥置换
        str_64 = chushizhihuan(str2bin(str_Ox));//将字符原文转换为01原文并执行初始置换
        for(j=0;j<16;j++){    
            memcpy(str_R_48,str_64+32,33);//分组
    
            miyuezuoyi(key_56,j);//4.密钥左移
            key_48 = miyueyasuozhihuan(key_56);//5.密钥压缩置换
            str_R_48 = kuozhanzhihuan(str_R_48);//6.扩展置换
            yihuoyunsuan(str_R_48,key_48,48);//7.48位异或运算
            str_R_48 = Shedaiti(str_R_48);//8.S盒代替
            str_R_48 = Phezhihuan(str_R_48);//9.P盒置换
            yihuoyunsuan(str_64,str_R_48,32);//10.32位异或运算
    
            if(j!=15){
                swap(str_64,str_64+32);
            }
        }
        str_64 = nichushizhihuan(str_64);
        str_Ox = bin2str(str_64);
        printf("%s\n",str_Ox);
    }
    return 0;
}

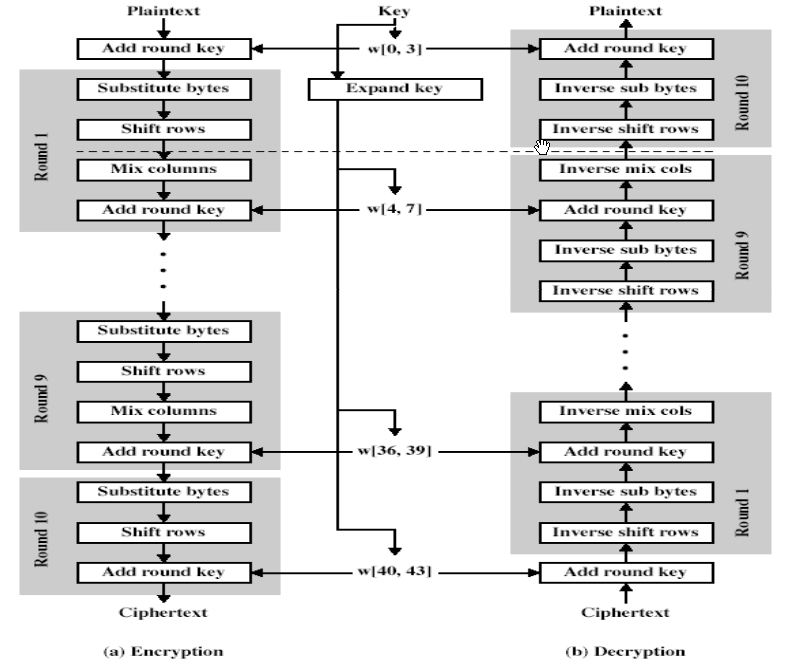
AES算法：

先搞定AES算法，基本变换包括SubBytes（字节替代）、ShiftRows（行移位）、MixColumns（列混淆）、AddRoundKey(轮密钥加）

其算法一般描述为

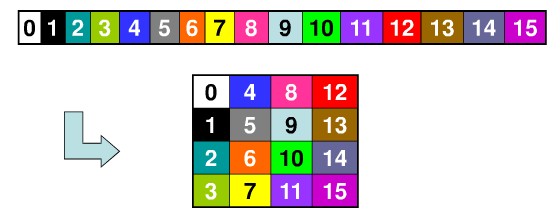
明文及密钥的组织排列方式

 

ByteSubstitution（字节替代）

非线性的字节替代，单独处理每个字节：

求该字节在有限域GF(28)上的乘法逆，"0"被映射为自身，即对于α∈GF(28)，求β∈GF(28)，

使得α·β=β·α=1mod(x8+x4+x2+x+1)。

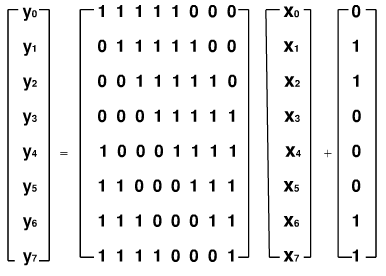
对上一步求得的乘法逆作仿射变换

yi=xi + x(i+4)mod8 + x(i+6)mod8 + x(i+7)mod8 + ci

(其中ci是6310即011000112的第i位），用矩阵表示为

本来打算把求乘法逆和仿射变换算法敲上去，最后还是放弃了…直接打置换表

  1. unsigned char sBox[] =
  2. { /*  0    1    2    3    4    5    6    7    8    9    a    b    c    d    e    f */
  3.     0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76, /*0*/
  4.     0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0, /*1*/
  5.     0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15, /*2*/
  6.     0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75, /*3*/
  7.     0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84, /*4*/
  8.     0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf, /*5*/
  9.     0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8, /*6*/
  10.     0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2, /*7*/
  11.     0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73, /*8*/
  12.     0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb, /*9*/
  13.     0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79, /*a*/
  14.     0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08, /*b*/
  15.     0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a, /*c*/
  16.     0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e, /*d*/
  17.     0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf, /*e*/
  18.     0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16  /*f*/
  19. };

下面是逆置换表，解密时使用

  1. unsigned char invsBox[256] =
  2. { /*  0    1    2    3    4    5    6    7    8    9    a    b    c    d    e    f  */
  3.     0x52,0x09,0x6a,0xd5,0x30,0x36,0xa5,0x38,0xbf,0x40,0xa3,0x9e,0x81,0xf3,0xd7,0xfb, /*0*/
  4.     0x7c,0xe3,0x39,0x82,0x9b,0x2f,0xff,0x87,0x34,0x8e,0x43,0x44,0xc4,0xde,0xe9,0xcb, /*1*/
  5.     0x54,0x7b,0x94,0x32,0xa6,0xc2,0x23,0x3d,0xee,0x4c,0x95,0x0b,0x42,0xfa,0xc3,0x4e, /*2*/
  6.     0x08,0x2e,0xa1,0x66,0x28,0xd9,0x24,0xb2,0x76,0x5b,0xa2,0x49,0x6d,0x8b,0xd1,0x25, /*3*/
  7.     0x72,0xf8,0xf6,0x64,0x86,0x68,0x98,0x16,0xd4,0xa4,0x5c,0xcc,0x5d,0x65,0xb6,0x92, /*4*/
  8.     0x6c,0x70,0x48,0x50,0xfd,0xed,0xb9,0xda,0x5e,0x15,0x46,0x57,0xa7,0x8d,0x9d,0x84, /*5*/
  9.     0x90,0xd8,0xab,0x00,0x8c,0xbc,0xd3,0x0a,0xf7,0xe4,0x58,0x05,0xb8,0xb3,0x45,0x06, /*6*/
  10.     0xd0,0x2c,0x1e,0x8f,0xca,0x3f,0x0f,0x02,0xc1,0xaf,0xbd,0x03,0x01,0x13,0x8a,0x6b, /*7*/
  11.     0x3a,0x91,0x11,0x41,0x4f,0x67,0xdc,0xea,0x97,0xf2,0xcf,0xce,0xf0,0xb4,0xe6,0x73, /*8*/
  12.     0x96,0xac,0x74,0x22,0xe7,0xad,0x35,0x85,0xe2,0xf9,0x37,0xe8,0x1c,0x75,0xdf,0x6e, /*9*/
  13.     0x47,0xf1,0x1a,0x71,0x1d,0x29,0xc5,0x89,0x6f,0xb7,0x62,0x0e,0xaa,0x18,0xbe,0x1b, /*a*/
  14.     0xfc,0x56,0x3e,0x4b,0xc6,0xd2,0x79,0x20,0x9a,0xdb,0xc0,0xfe,0x78,0xcd,0x5a,0xf4, /*b*/
  15.     0x1f,0xdd,0xa8,0x33,0x88,0x07,0xc7,0x31,0xb1,0x12,0x10,0x59,0x27,0x80,0xec,0x5f, /*c*/
  16.     0x60,0x51,0x7f,0xa9,0x19,0xb5,0x4a,0x0d,0x2d,0xe5,0x7a,0x9f,0x93,0xc9,0x9c,0xef, /*d*/
  17.     0xa0,0xe0,0x3b,0x4d,0xae,0x2a,0xf5,0xb0,0xc8,0xeb,0xbb,0x3c,0x83,0x53,0x99,0x61, /*e*/
  18.     0x17,0x2b,0x04,0x7e,0xba,0x77,0xd6,0x26,0xe1,0x69,0x14,0x63,0x55,0x21,0x0c,0x7d  /*f*/
  19. };

这 里遇到问题了，本来用纯c初始化数组很正常，封装成类以后发现不能初始化，不管是声明、构造函数都无法初始化，百歌谷度了一通后没有任何答案，无奈只能在 构造函数中声明一个局部变量数组并初始化，然后用memcpy，（成员变量名为Sbox/InvSbox，局部变量名sBox/invsBox）

  1. void AES::SubBytes(unsigned char state[][4])
  2. {
  3.     int r,c;
  4.     for(r=0; r<4; r++)
  5.     {
  6.         for(c=0; c<4; c++)
  7.         {
  8.             state[r][c] = Sbox[state[r][c]];
  9.         }
  10.     }
  11. }

 

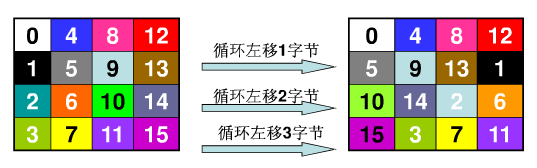
ShiftRows（行移位变换）

行移位变换完成基于行的循环位移操作，变换方法：

即行移位变换作用于行上，第0行不变，第1行循环左移1个字节，第2行循环左移2个字节，第3行循环左移3个字节。

  1. void AES::ShiftRows(unsigned char state[][4])
  2. {
  3.     unsigned char t[4];
  4.     int r,c;
  5.     for(r=1; r<4; r++)
  6.     {
  7.         for(c=0; c<4; c++)
  8.         {
  9.             t[c] = state[r][(c+r)%4];
  10.         }
  11.         for(c=0; c<4; c++)
  12.         {
  13.             state[r][c] = t[c];
  14.         }
  15.     }
  16. }

 

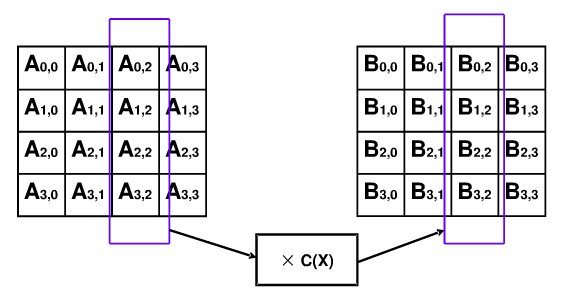
MixColumns（列混淆变换）

逐列混合，方法：

b(x) = (03·x3 + 01·x2 + 01·x + 02) · a(x) mod(x4 + 1)

矩阵表示形式：

  1. void AES::MixColumns(unsigned char state[][4])
  2. {
  3.     unsigned char t[4];
  4.     int r,c;
  5.     for(c=0; c< 4; c++)
  6.     {
  7.         for(r=0; r<4; r++)
  8.         {
  9.             t[r] = state[r][c];
  10.         }
  11.         for(r=0; r<4; r++)
  12.         {
  13.             state[r][c] = FFmul(0x02, t[r])
  14.                         ^ FFmul(0x03, t[(r+1)%4])
  15.                         ^ FFmul(0x01, t[(r+2)%4])
  16.                         ^ FFmul(0x01, t[(r+3)%4]);
  17.         }
  18.     }
  19. }
  20. unsigned char AES::FFmul(unsigned char a, unsigned char b)
  21. {
  22.     unsigned char bw[4];
  23.     unsigned char res=0;
  24.     int i;
  25.     bw[0] = b;
  26.     for(i=1; i<4; i++)
  27.     {
  28.         bw[i] = bw[i-1]<<1;
  29.         if(bw[i-1]&0x80)
  30.         {
  31.             bw[i]^=0x1b;
  32.         }
  33.     }
  34.     for(i=0; i<4; i++)
  35.     {
  36.         if((a>>i)&0x01)
  37.         {
  38.             res ^= bw[i];
  39.         }
  40.     }
  41.     return res;
  42. }

其中FFmul为有限域GF(28)上的乘法，标准算法应该是循环8次（b与a的每一位相乘，结果相加），但这里只用到最低2位，解密时用到的逆列混淆也只用了低4位，所以在这里高4位的运算是多余的，只计算低4位。

 

AddRoundKey（轮密钥加变换）

简单来说就是逐字节相加，有限域GF(28)上的加法是模2加法，即异或

  1. void AES::AddRoundKey(unsigned char state[][4], unsigned char k[][4])
  2. {
  3.     int r,c;
  4.     for(c=0; c<4; c++)
  5.     {
  6.         for(r=0; r<4; r++)
  7.         {
  8.             state[r][c] ^= k[r][c];
  9.         }
  10.     }
  11. }

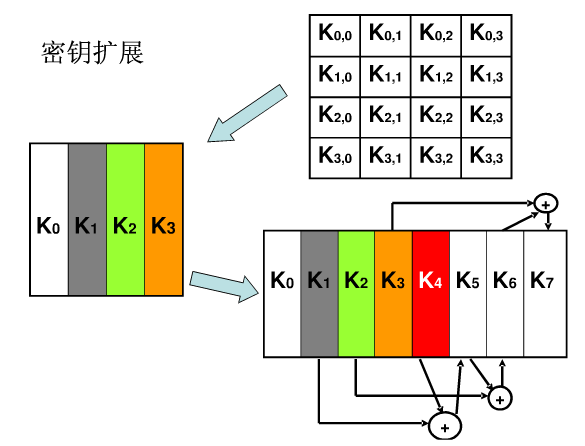
KeyExpansion（密钥扩展）

将输入的密钥扩展为11组128位密钥组，其中第0组为输入密钥本身

其后第n组第i列 为 第n-1组第i列 与 第n组第i-1列之和（模2加法，1<= i <=3）

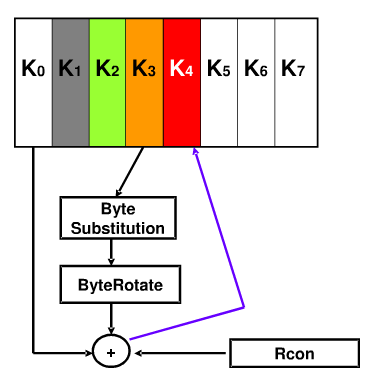
对于每一组 第一列即i=0，有特殊的处理

将前一列即第n-1组第3列的4个字节循环左移1个字节，

并对每个字节进行字节替代变换SubBytes

将第一行（即第一个字节）与轮常量rc[n]相加

最后再与前一组该列相加

  1. void AES::KeyExpansion(unsigned char* key, unsigned char w[][4][4])
  2. {
  3.     int i,j,r,c;
  4.     unsigned char rc[] = {0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36};
  5.     for(r=0; r<4; r++)
  6.     {
  7.         for(c=0; c<4; c++)
  8.         {
  9.             w[0][r][c] = key[r+c*4];
  10.         }
  11.     }
  12.     for(i=1; i<=10; i++)
  13.     {
  14.         for(j=0; j<4; j++)
  15.         {
  16.             unsigned char t[4];
  17.             for(r=0; r<4; r++)
  18.             {
  19.                 t[r] = j ? w[i][r][j-1] : w[i-1][r][3];
  20.             }
  21.             if(j == 0)
  22.             {
  23.                 unsigned char temp = t[0];
  24.                 for(r=0; r<3; r++)
  25.                 {
  26.                     t[r] = Sbox[t[(r+1)%4]];
  27.                 }
  28.                 t[3] = Sbox[temp];
  29.                 t[0] ^= rc[i-1];
  30.             }
  31.             for(r=0; r<4; r++)
  32.             {
  33.                 w[i][r][j] = w[i-1][r][j] ^ t[r];
  34.             }
  35.         }
  36.     }
  37. }

解密的基本运算

AES解密算法与加密不同，基本运算中除了AddRoundKey（轮密钥加）不变外，其余的都需要进行逆变换，即

InvSubBytes（逆字节替代）、InvShiftRows（逆行移位）、InvMixColumns（逆列混淆）

  1. void AES::InvSubBytes(unsigned char state[][4])
  2. {
  3.     int r,c;
  4.     for(r=0; r<4; r++)
  5.     {
  6.         for(c=0; c<4; c++)
  7.         {
  8.             state[r][c] = InvSbox[state[r][c]];
  9.         }
  10.     }
  11. }
  12. void AES::InvShiftRows(unsigned char state[][4])
  13. {
  14.     unsigned char t[4];
  15.     int r,c;
  16.     for(r=1; r<4; r++)
  17.     {
  18.         for(c=0; c<4; c++)
  19.         {
  20.             t[c] = state[r][(c-r+4)%4];
  21.         }
  22.         for(c=0; c<4; c++)
  23.         {
  24.             state[r][c] = t[c];
  25.         }
  26.     }
  27. }
  28. void AES::InvMixColumns(unsigned char state[][4])
  29. {
  30.     unsigned char t[4];
  31.     int r,c;
  32.     for(c=0; c< 4; c++)
  33.     {
  34.         for(r=0; r<4; r++)
  35.         {
  36.             t[r] = state[r][c];
  37.         }
  38.         for(r=0; r<4; r++)
  39.         {
  40.             state[r][c] = FFmul(0x0e, t[r])
  41.                         ^ FFmul(0x0b, t[(r+1)%4])
  42.                         ^ FFmul(0x0d, t[(r+2)%4])
  43.                         ^ FFmul(0x09, t[(r+3)%4]);
  44.         }
  45.     }
  46. }

加密过程

先将输入的明文按列序组合成4*4的矩阵，直接与第0组密钥（即输入的密钥）相加（异或），作为轮加密的输入

然后循环10次进行SubBytes、ShiftRows、MixColumns、AddRoundKey运算，最后恢复原序列

需要注意的是最后一轮并不进行MixColumns（列混淆变换）

  1. unsigned char* AES::Cipher(unsigned char* input)
  2. {
  3.     unsigned char state[4][4];
  4.     int i,r,c;
  5.     for(r=0; r<4; r++)
  6.     {
  7.         for(c=0; c<4 ;c++)
  8.         {
  9.             state[r][c] = input[c*4+r];
  10.         }
  11.     }
  12.     AddRoundKey(state,w[0]);
  13.     for(i=1; i<=10; i++)
  14.     {
  15.         SubBytes(state);
  16.         ShiftRows(state);
  17.         if(i!=10)MixColumns(state);
  18.         AddRoundKey(state,w[i]);
  19.     }
  20.     for(r=0; r<4; r++)
  21.     {
  22.         for(c=0; c<4 ;c++)
  23.         {
  24.             input[c*4+r] = state[r][c];
  25.         }
  26.     }
  27.     return input;
  28. }

解密过程

  1. unsigned char* AES::InvCipher(unsigned char* input)
  2. {
  3.     unsigned char state[4][4];
  4.     int i,r,c;
  5.     for(r=0; r<4; r++)
  6.     {
  7.         for(c=0; c<4 ;c++)
  8.         {
  9.             state[r][c] = input[c*4+r];
  10.         }
  11.     }
  12.     AddRoundKey(state, w[10]);
  13.     for(i=9; i>=0; i--)
  14.     {
  15.         InvShiftRows(state);
  16.         InvSubBytes(state);
  17.         AddRoundKey(state, w[i]);
  18.         if(i)InvMixColumns(state);
  19.     }
  20.     for(r=0; r<4; r++)
  21.     {
  22.         for(c=0; c<4 ;c++)
  23.         {
  24.             input[c*4+r] = state[r][c];
  25.         }
  26.     }
  27.     return input;
  28. }

对外部数据的加密/解密

至此已经实现了AES加密与解密的原型，在使用的时候一般处理的是字符串等，而不是直接传入128位的数据，所以要封装一下对外部数据的加解密处理

  1. void* AES::Cipher(void* input, int length)
  2. {
  3.     unsigned char* in = (unsigned char*) input;
  4.     int i;
  5.     if(!length)
  6.     {
  7.         while(*(in+length++));
  8.         in = (unsigned char*) input;
  9.     }
  10.     for(i=0; i<length; i+=16)  < span="">
  11.     {
  12.         Cipher(in+i);
  13.     }
  14.     return input;
  15. }
  16. void* AES::InvCipher(void* input, int length)
  17. {
  18.     unsigned char* in = (unsigned char*) input;
  19.     int i;
  20.     for(i=0; i<length; i+=16)  < span="">
  21.     {
  22.         InvCipher(in+i);
  23.     }
  24.     return input;
  25. }

加密时默认参数length=0,为要加密的数据长度，如果使用默认值，则作为字符串处理，以"为结尾计算长度

加密时传进的指针要预留够16整数倍字节的空间，因为加密操作直接修改原数据，不足128位可能造成内存溢出

SHA算法：

1 SHA1算法简介

安全哈希算法（Secure Hash Algorithm）主要适用于数字签名标准（Digital Signature Standard DSS）里面定义的数字签名算法（Digital Signature Algorithm DSA）。对于长度小于2^64位的消息，SHA1会产生一个160位的消息摘要。当接收到消息的时候，这个消息摘要可以用来验证数据的完整性。在传输的 过程中，数据很可能会发生变化，那么这时候就会产生不同的消息摘要。

SHA1有如下特性：不可以从消息摘要中复原信息；两个不同的消息不会产生同样的消息摘要。

2 术语和概念

2.1位(Bit)，字节（Byte）和字（Word）

SHA1始终把消息当成一个位（bit）字符串来处理。本文中，一个“字”（Word）是32位，而一个“字节”（Byte）是8位。比如，字符串 “abc”可以被转换成一个位字符串：01100001 01100010 01100011。它也可以被表示成16进制字符串: 0x616263.

2.2 运算符和符号

下面的逻辑运算符都被运用于“字”（Word）

X^Y = X，Y逻辑与

X / Y = X，Y逻辑或

X XOR Y= X，Y逻辑异或

~X = X逻辑取反

X+Y定义如下：

字X 和Y 代表两个整数x 和y, 其中0 <= x < 2^32 且0 <= y < 2^32. 令整数z = (x + y) mod 2^32. 这时候0 <= z < 2^32. 将z转换成字Z, 那么就是Z = X + Y. www.2cto.com

循环左移位操作符Sn(X)。X是一个字，n是一个整数，0<=n<=32。Sn(X) = (X<>32-n)

X<>n是抛弃右边的n位，将各个位依次向右移动n位，然后在左边的n位填0。因此可以叫Sn(X)位循环移位运算

3 SHA1算法描述

在SHA1算法中，我们必须把原始消息（字符串，文件等）转换成位字符串。SHA1算法只接受位作为输入。假设我们对字符串“abc”产生消息摘要。首先，我们将它转换成位字符串如下：

01100001 01100010 01100011

―――――――――――――

‘a’=97 ‘b’=98 ‘c’=99

这个位字符串的长度为24。下面我们需要5个步骤来计算MD5。

3.1 补位

消息必须进行补位，以使其长度在对512取模以后的余数是448。也就是说，（补位后的消息长度）%512 = 448。即使长度已经满足对512取模后余数是448，补位也必须要进行。

补位是这样进行的：先补一个1，然后再补0，直到长度满足对512取模后余数是448。总而言之，补位是至少补一位，最多补512位。还是以前面的“abc”为例显示补位的过程。

原始信息：01100001 01100010 01100011

补位第一步：01100001 01100010 01100011 1

首先补一个“1”

补位第二步：01100001 01100010 01100011 10…..0

然后补423个“0”

我们可以把最后补位完成后的数据用16进制写成下面的样子

61626380 00000000 00000000 00000000

00000000 00000000 00000000 00000000

00000000 00000000 00000000 00000000

00000000 00000000

现在，数据的长度是448了，我们可以进行下一步操作。

3.2 补长度

所谓的补长度是将原始数据的长度补到已经进行了补位操作的消息后面。通常用一个64位的数据来表示原始消息的长度。如果消息长度不大于2^64，那么第一个字就是0。在进行了补长度的操作以后，整个消息就变成下面这样了（16进制格式）

61626380 00000000 00000000 00000000

00000000 00000000 00000000 00000000

00000000 00000000 00000000 00000000

00000000 00000000 00000000 00000018

如果原始的消息长度超过了512，我们需要将它补成512的倍数。然后我们把整个消息分成一个一个512位的数据块，分别处理每一个数据块，从而得到消息摘要。

3.3 使用的常量

一系列的常量字K(0), K(1), … , K(79)，如果以16进制给出。它们如下：

Kt = 0x5A827999 (0 <= t <= 19)

Kt = 0x6ED9EBA1 (20 <= t <= 39)

Kt = 0x8F1BBCDC (40 <= t <= 59)

Kt = 0xCA62C1D6 (60 <= t <= 79).

3.4 需要使用的函数

在SHA1中我们需要一系列的函数。每个函数ft (0 <= t <= 79)都操作32位字B，C，D并且产生32位字作为输出。ft(B,C,D)可以如下定义

ft(B,C,D) = (B AND C) or ((NOT B) AND D) ( 0 <= t <= 19)

ft(B,C,D) = B XOR C XOR D (20 <= t <= 39)

ft(B,C,D) = (B AND C) or (B AND D) or (C AND D) (40 <= t <= 59)

ft(B,C,D) = B XOR C XOR D (60 <= t <= 79).

3.5 计算消息摘要

必须使用进行了补位和补长度后的消息来计算消息摘要。计算需要两个缓冲区，每个都由5个32位的字组成，还需要一个80个32位字的缓冲区。第一个5个字的缓冲区被标识为A，B，C，D，E。第二个5个字的缓冲区被标识为H0, H1, H2, H3, H4

。80个字的缓冲区被标识为W0, W1,…, W79

另外还需要一个一个字的TEMP缓冲区。

为了产生消息摘要，在第4部分中定义的16个字的数据块M1, M2,…, Mn

会依次进行处理，处理每个数据块Mi 包含80个步骤。

在处理每个数据块之前，缓冲区{Hi} 被初始化为下面的值（16进制）

H0 = 0x67452301

H1 = 0xEFCDAB89

H2 = 0x98BADCFE

H3 = 0x10325476

H4 = 0xC3D2E1F0.

现在开始处理M1, M2, … , Mn。为了处理Mi,需要进行下面的步骤

(1).将Mi 分成16 个字W0, W1, … , W15, W0 是最左边的字

(2).对于t = 16 到79 令Wt = S1(Wt-3 XOR Wt-8 XOR Wt- 14 XOR Wt-16).

(3).令A = H0, B = H1, C = H2, D = H3, E = H4.

(4) 对于t = 0 到79，执行下面的循环

TEMP = S5(A) + ft(B,C,D) + E + Wt + Kt;

E = D; D = C; C = S30(B); B = A; A = TEMP;

(5).令H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E.

在处理完所有的Mn, 后，消息摘要是一个160位的字符串，以下面的顺序标识

H0 H1 H2 H3 H4.

对于SHA256,SHA384,SHA512。你也可以用相似的办法来计算消息摘要。对消息进行补位的算法完全是一样的。

  1. public class SHA1Util {
  2. private static final boolean hexcase = false;
  3. private static final String b64pad = "=";
  4. private static final int chrsz = 8;
  5. // 得到字符串SHA-1值的方法
  6. public static String hex_sha1(String s) {
  7.         s = (s == null) ? "" : s;
  8. return binb2hex(core_sha1(str2binb(s), s.length() * chrsz));
  9.     }
  10. public static String b64_hmac_sha1(String key, String data) {
  11. return binb2b64(core_hmac_sha1(key, data));
  12.     }
  13. public static String b64_sha1(String s) {
  14.         s = (s == null) ? "" : s;
  15. return binb2b64(core_sha1(str2binb(s), s.length() * chrsz));
  16.     }
  17. private static String binb2b64(int[] binarray) {
  18.         String tab = "abcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyz0123456789+/";
  19.         String str = "";
  20.         binarray = strechbinarray(binarray, binarray.length * 4);
  21. for (int i = 0; i < binarray.length * 4; i += 3) {
  22. int triplet = (((binarray[i >> 2] >> 8 * (3 – i % 4)) & 0xff) << 16)
  23.                     | (((binarray[i + 1 >> 2] >> 8 * (3 – (i + 1) % 4)) & 0xff) << 8)
  24.                     | ((binarray[i + 2 >> 2] >> 8 * (3 – (i + 2) % 4)) & 0xff);
  25. for (int j = 0; j < 4; j++) {
  26. if (i * 8 + j * 6 > binarray.length * 32) {
  27.                     str += b64pad;
  28.                 } else {
  29.                     str += tab.charAt((triplet >> 6 * (3 – j)) & 0x3f);
  30.                 }
  31.             }
  32.         }
  33. return cleanb64str(str);
  34.     }
  35. private static String binb2hex(int[] binarray) {
  36.         String hex_tab = hexcase ? "0123456789abcdef" : "0123456789abcdef";
  37.         String str = "";
  38. for (int i = 0; i < binarray.length * 4; i++) {
  39. char a = (char) hex_tab.charAt((binarray[i >> 2] >> ((3 – i % 4) * 8 + 4)) & 0xf);
  40. char b = (char) hex_tab.charAt((binarray[i >> 2] >> ((3 – i % 4) * 8)) & 0xf);
  41.             str += (new Character(a).toString() + new Character(b).toString());
  42.         }
  43. return str;
  44.     }
  45. private static String binb2str(int[] bin) {
  46.         String str = "";
  47. int mask = (1 << chrsz) – 1;
  48. for (int i = 0; i < bin.length * 32; i += chrsz) {
  49.             str += (char) ((bin[i >> 5] >>> (24 – i % 32)) & mask);
  50.         }
  51. return str;
  52.     }
  53. private static int bit_rol(int num, int cnt) {
  54. return (num << cnt) | (num >>> (32 – cnt));
  55.     }
  56. private static String cleanb64str(String str) {
  57.         str = (str == null) ? "" : str;
  58. int len = str.length();
  59. if (len <= 1) {
  60. return str;
  61.         }
  62. char trailchar = str.charAt(len – 1);
  63.         String trailstr = "";
  64. for (int i = len – 1; i >= 0 && str.charAt(i) == trailchar; i--) {
  65.             trailstr += str.charAt(i);
  66.         }
  67. return str.substring(0, str.indexOf(trailstr));
  68.     }
  69. private static int[] complete216(int[] oldbin) {
  70. if (oldbin.length >= 16) {
  71. return oldbin;
  72.         }
  73. int[] newbin = new int[16 – oldbin.length];
  74. for (int i = 0; i < newbin.length; newbin[i] = 0, i++)
  75.             ;
  76. return concat(oldbin, newbin);
  77.     }
  78. private static int[] concat(int[] oldbin, int[] newbin) {
  79. int[] retval = new int[oldbin.length + newbin.length];
  80. for (int i = 0; i < (oldbin.length + newbin.length); i++) {
  81. if (i < oldbin.length) {
  82.                 retval[i] = oldbin[i];
  83.             } else {
  84.                 retval[i] = newbin[i – oldbin.length];
  85.             }
  86.         }
  87. return retval;
  88.     }
  89. private static int[] core_hmac_sha1(String key, String data) {
  90.         key = (key == null) ? "" : key;
  91.         data = (data == null) ? "" : data;
  92. int[] bkey = complete216(str2binb(key));
  93. if (bkey.length > 16) {
  94.             bkey = core_sha1(bkey, key.length() * chrsz);
  95.         }
  96. int[] ipad = new int[16];
  97. int[] opad = new int[16];
  98. for (int i = 0; i < 16; ipad[i] = 0, opad[i] = 0, i++)
  99.             ;
  100. for (int i = 0; i < 16; i++) {
  101.             ipad[i] = bkey[i] ^ 0x36363636;
  102.             opad[i] = bkey[i] ^ 0x5c5c5c5c;
  103.         }
  104. int[] hash = core_sha1(concat(ipad, str2binb(data)), 512 + data.length() * chrsz);
  105. return core_sha1(concat(opad, hash), 512 + 160);
  106.     }
  107. private static int[] core_sha1(int[] x, int len) {
  108. int size = (len >> 5);
  109.         x = strechbinarray(x, size);
  110.         x[len >> 5] |= 0x80 << (24 – len % 32);
  111.         size = ((len + 64 >> 9) << 4) + 15;
  112.         x = strechbinarray(x, size);
  113.         x[((len + 64 >> 9) << 4) + 15] = len;
  114. int[] w = new int[80];
  115. int a = 1732584193;
  116. int b = –271733879;
  117. int c = –1732584194;
  118. int d = 271733878;
  119. int e = –1009589776;
  120. for (int i = 0; i < x.length; i += 16) {
  121. int olda = a;
  122. int oldb = b;
  123. int oldc = c;
  124. int oldd = d;
  125. int olde = e;
  126. for (int j = 0; j < 80; j++) {
  127. if (j < 16) {
  128.                     w[j] = x[i + j];
  129.                 } else {
  130.                     w[j] = rol(w[j – 3] ^ w[j – 8] ^ w[j – 14] ^ w[j – 16], 1);
  131.                 }
  132. int t = safe_add(safe_add(rol(a, 5), sha1_ft(j, b, c, d)), safe_add(safe_add(e, w[j]), sha1_kt(j)));
  133.                 e = d;
  134.                 d = c;
  135.                 c = rol(b, 30);
  136.                 b = a;
  137.                 a = t;
  138.             }
  139.             a = safe_add(a, olda);
  140.             b = safe_add(b, oldb);
  141.             c = safe_add(c, oldc);
  142.             d = safe_add(d, oldd);
  143.             e = safe_add(e, olde);
  144.         }
  145. int[] retval = new int[5];
  146.         retval[0] = a;
  147.         retval[1] = b;
  148.         retval[2] = c;
  149.         retval[3] = d;
  150.         retval[4] = e;
  151. return retval;
  152.     }
  153. private static void dotest() {
  154.         String key = "key";
  155.         String data = "data";
  156.         System.out.println("hex_sha1(" + data + ")=" + hex_sha1(data));
  157.         System.out.println("b64_sha1(" + data + ")=" + b64_sha1(data));
  158.         System.out.println("str_sha1(" + data + ")=" + str_sha1(data));
  159.         System.out.println("hex_hmac_sha1(" + key + "," + data + ")=" + hex_hmac_sha1(key, data));
  160.         System.out.println("b64_hmac_sha1(" + key + "," + data + ")=" + b64_hmac_sha1(key, data));
  161.         System.out.println("str_hmac_sha1(" + key + "," + data + ")=" + str_hmac_sha1(key, data));
  162.     }
  163. public static String hex_hmac_sha1(String key, String data) {
  164. return binb2hex(core_hmac_sha1(key, data));
  165.     }
  166. private static int rol(int num, int cnt) {
  167. return (num << cnt) | (num >>> (32 – cnt));
  168.     }
  169. private static int safe_add(int x, int y) {
  170. int lsw = (int) (x & 0xffff) + (int) (y & 0xffff);
  171. int msw = (x >> 16) + (y >> 16) + (lsw >> 16);
  172. return (msw << 16) | (lsw & 0xffff);
  173.     }
  174. private static int sha1_ft(int t, int b, int c, int d) {
  175. if (t < 20)
  176. return (b & c) | ((~b) & d);
  177. if (t < 40)
  178. return b ^ c ^ d;
  179. if (t < 60)
  180. return (b & c) | (b & d) | (c & d);
  181. return b ^ c ^ d;
  182.     }
  183. private static int sha1_kt(int t) {
  184. return (t < 20) ? 1518500249 : (t < 40) ? 1859775393 : (t < 60) ? –1894007588 : –899497514;
  185.     }
  186. private static boolean sha1_vm_test() {
  187. return hexcase ? hex_sha1("abc").equals("a9993e364706816aba3e25717850c26c9cd0d89d") : hex_sha1("abc").equals(
  188. "a9993e364706816aba3e25717850c26c9cd0d89d");
  189.     }
  190. public static String str_hmac_sha1(String key, String data) {
  191. return binb2str(core_hmac_sha1(key, data));
  192.     }
  193. public static String str_sha1(String s) {
  194.         s = (s == null) ? "" : s;
  195. return binb2str(core_sha1(str2binb(s), s.length() * chrsz));
  196.     }
  197. private static int[] str2binb(String str) {
  198.         str = (str == null) ? "" : str;
  199. int[] tmp = new int[str.length() * chrsz];
  200. int mask = (1 << chrsz) – 1;
  201. for (int i = 0; i < str.length() * chrsz; i += chrsz) {
  202.             tmp[i >> 5] |= ((int) (str.charAt(i / chrsz)) & mask) << (24 – i % 32);
  203.         }
  204. int len = 0;
  205. for (int i = 0; i < tmp.length && tmp[i] != 0; i++, len++)
  206.             ;
  207. int[] bin = new int[len];
  208. for (int i = 0; i < len; i++) {
  209.             bin[i] = tmp[i];
  210.         }
  211. return bin;
  212.     }
  213. private static int[] strechbinarray(int[] oldbin, int size) {
  214. int currlen = oldbin.length;
  215. if (currlen >= size + 1) {
  216. return oldbin;
  217.         }
  218. int[] newbin = new int[size + 1];
  219. for (int i = 0; i < size; newbin[i] = 0, i++)
  220.             ;
  221. for (int i = 0; i < currlen; i++) {
  222.             newbin[i] = oldbin[i];
  223.         }
  224. return newbin;
  225.     }
  226. public static void main(String args[]) {
  227.         System.out.println("admin的SHA1的值为：" + hex_sha1("admin") + ",length=" + hex_sha1("admin").length());
  228.     }
  229. }

from:https://blog.csdn.net/aa2397199142/article/details/50844879

Copyright © 2024 Longsheng All rights reserved.